I recently rolled up a few characters for an upcoming campaign. These characters will be used by a group of people who have played B/X D&D and 1ed AD&D in the past, but haven’t played much or at all in the last 20 years. The resulting ability scores were on the anemic side, and since these players were not hardened veterans, and I wanted them to have fun instead of fighting with sub-par character stats all night, I decided to experiment with other ways of rolling up ability scores to see if I could come up with some more palatable characters.
The first option was to just pick numbers out of the air, but the lack of randomness made it no fun and all characters tended to be the same. So I went to a hunt to try to find alternative methods, and I derived a couple of my own. These methods are outlined below, along with some of the basics that you already know about. Keep in mind this article only considers rolling ability scores for OD&D, B/X, 1ed, and 2ed. My scant knowledge of 3, 3.5, and 4ed tells me that these methods can have drawbacks when used for those editions, but I really have no idea and don’t care.
Old school: When I started playing with the Holmes basic set in 1980, the ONLY method was to roll 3d6 and take the scores in order (str, int, wis, dex, con, chr). If you rolled three ones, then that ability score was three. And if you wanted to play a thief, but your rolls dictated that this character should be a magic-user, then you played a magic-user. Suck it up, nerd! This is fine for the hardcore gamer that is willing to deal with potentially bad scores and takes it as a challenge. But for the unseasoned player who just wants a night of fun and most likely will not use this character again, this isn’t the best option. This method will generate scores of 3-18.
The Standard: The player rolls 4d6 and DROPS the lowest die, and the resulting scores can be arranged as desired. This seems to be the most widely used method, at least with the groups that I’ve played with and other people I’ve talked to. By allowing the player to arrange the scores, it allows him or her to play whatever class is desired, as he or she can assign the best roll to the prime requisite for that class. While this is a better option than the old school method, it can still create a character with more than one low ability score if the dice are feeling nasty. Blurgh! Again, the possible scores generated with this method are 3-18, but the chance of rolling the lower end of the range is less, as the mean is higher than the old school method.
The ‘Hero’: This is one that I discovered recently while reading the Pathfinder SRD. The method is to roll 2d6 and add 6 to the roll and arrange the scores as desired. Scores will fall in the range of 8-18, which means no attribute will have any negative bonuses. While I haven’t used this method as a player or a DM, on the surface it seems like it would work well, and would live up to its name. A slight modification to this method would be to roll 3d6, dropping the lowest score, and then adding 6.
Modified Hero: Each ability score starts at 8. Seven dice are rolled and added to the ability scores as seen fit by the player. The full amount of each die must be used in this method. For example, if two sixes are rolled, the player cannot add both to the base of eight and drop the extra two points to get a score of 18. All points must be used. This is another interesting option that might have some great possibilities. No score will be less than 8, and if the dice are friendly, one or more 18s is very possible.
Old school alternates: Roll 3d6 12 times, taking the highest six results, and arranging them how the player sees fit. Or, roll 3d6 six times for each attribute, and the highest scores are kept. This results in 36 dice rolls, which is not only time-consuming but can become confusing to the uninitiated
Pyramids: I’ve named this method because it works as such: roll 3d4 and add 6 to the result. This is an interesting method that will result in hero-like scores. The curve resulted from rolling with this method has steep sides, like a pyramid, and decent mean values. Also, the d4s are like little pyramids. See how I did that? The range here is 9-18.
Point buy: Each attribute has a base value of 8. 25 points (or more or less, as determined by the DM) are then given to ‘buy’ higher scores. The cost is point for point up to 14 (or 13 or 15, again at the DMs discretion), with two points needed for each attribute point desired above 14. Thus, to achieve an attribute score of 18 would cost 14 points of the 25 granted (6 points for 9-14, 8 points for 15-18). This method could be modified greatly. For example, point buying is point for point from 9 to 14, then 15 and 16 cost 2 points, 17 and 18 costs 3 points each. This method could burn thru points quickly, so the DM might grant 30 instead of 25. The possibilities are virtually endless with this method.
Modified point buy: Roll 3d6 (or 4d6, dropping the lowest) per attribute, arrange as desired. The player is given a pool of six more points to add to one or more attributes as seen fit. The range here is 3-18, but some low scores can be bolstered with the additional points. Again, hero-like characters can be generated pretty easily, and this can be modified as the DM sees fit (the pool of available points could be 8, or maybe 10).
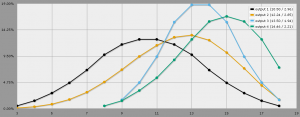
I’ve used Any Dice (http://anydice.com/) to generate a graph that overlays four of the attribute rolling methods discussed above. Each line shows the probability of achieving a certain value, and the most probable values are revealed at the top of each curve. (Click the graph to see a larger version.)
The black line is the old school method. As you can see, the curve is evenly spread along the X-axis, with the mean values being 10 and 11. The orange line represents the standard method. The mean here is 13, but the range of possible values is the same as the black line, and there is a slightly higher chance of rolling an 18. The blue line shows the possible results of the pyramids method. The range is much shorter from the first two, being 9-18 and the median values are 13 and 14.
Finally, I threw in the green line for fun. This is an interesting method that I discussed above in the hero method: roll 3d6, drop the lowest die, and add 6. The median here is 15 with a pretty high probability, and the chance of rolling 18 is the highest of all four. The range is also short: 8-18, which will ensure that no matter what edition you’re playing, none of the PCs attributes will result in a penalty.
Once scores are achieved, some DMs may want to give the players options for adjusting scores further. For example, if a player wants a higher dexterity, he or she can gain one point of dexterity, but will have to give up two (or more) points of another score. This option is viable if the player really wants to hit a certain bonus threshold with one or more attributes, or needs a certain score for a attribute based on racial profile.
In the end, there are so many methods of achieving character attributes that they cannot all be outlined here. I’m going to try the hero method on my next batch of pre-gen characters, and we’ll see how it goes. The true test will come when the play begins.